It's Alive! HV DC Supply is Fully Functional

After roughly half a year of design and troubleshooting, I finished fully testing my custom variable high voltage DC power supply yesterday. The supply is capable of producing up to 20 kV at 10 mA. I will be using it to charge my high-voltage capacitor bank and hopefully explode some water.

The finished and tested circuit

The circuit is essentially comprised of three subsystems: a DC mains supply, an H-bridge inverter, and a high-voltage multiplying rectifier. The first is visible in the top portion of the above photo. It's just your basic diode bridge rectifier, with a 60 Vp sinusoidal input and nearly 1000 uF of smoothing capacitance.

The H-bridge inverter can be seen in the middle of the photo. Its driving frequency can be varied between discreet values ranging from 40 to 47 kHz using the rotary switch visible towards the bottom of the shot. This small range of driving frequencies corresponds to a large range of output voltages (from about 8 to 20 kV), as my flyback transformer (not visible in the above photo) resonates at near 60 kHz. This phenomenon is illustrated below:

Above resonance

At resonance

Below resonance

The circuit's business end, the high voltage output stage, is depicted below:

Parts are (from left): flyback transformer, Crockoft Walton multiplier, protective diodes, output resistors

In order to prevent arcing between and within the high-voltage components, I had to submerge them all in mineral oil. While messy, this method was extremely effective at insulating the parts.

The small, innocuous-looking flyback transformer I used in my circuit is somewhat unconventional. Most HV hobbyists think of the large suction-cup sporting flyback transformers found in CRT's when they hear the term (see picture below). These transformers are frequently used to make spark generators and are easy to salvage from old TV's and computer monitors. They are generally much beefier than the downsized flyback I used in my supply, and one would expect to get more voltage from them.  I experimented with using one of these in my supply, but ultimately decided against it. All such flyback transformers I found were internally rectified (AC flybacks were outmoded in TV's thirty years ago) and therefore could not be used with my CW multiplying rectifier. So despite the traditional flyback's heft, I was able to get a greater voltage output from my miniaturized version by tacking a voltage multiplier onto its AC output.  

A classic flyback transformer, salvaged from an old computer monitor

Troubleshooting my circuit was hardly mundane; between prototypes, my circuit experienced some catastrophic failures. The aftermath of one is pictured below:

Casualties: four power transistors, one LCM555 timer, one breadboard

I was testing the circuit at the limits of its operating range, and I neglected to account for the heat my driving transistors would accrue. After operating for about five seconds, the transistors promptly burst into flames. Let it be known: the large heatsinks visible in the first picture are there for a reason!

Assuming my circuit doesn't spontaneously combust again any time in the near future, I will be using it to (carefully!) charge up some gargantuan high-voltage oil filled capacitors (see below). Once I'm confident  I can charge and discharge these monsters safely, I'll hook up my makeshift water accelerator barrel, and we'll see if I can replicate Peter Graneau's overunity water arc explosions.

Back to the Drawing Board: Making my own High Voltage Supply

Don't think I've been spending all that time since my last post idly!

That couldn't be farther from the truth. These past 6 months I've been laboring over a little circuit of mine, a custom high voltage power supply that should be able to source all the power I need to blow up some water. The power supply is built entirely from scratch and took a lot of troubleshooting to get working. And, it's not quite done yet, but its completion is in sight.

I will elaborate on the circuit later when the designs have finalized and thoroughly tested.

The system's components are outlined below (click for larger image):

Finally, some quick snapshots of the physical circuit:

Custom DC supply (from 120V mains):

110-90V tapped mains transformer

High-current 120 Vp rectifier, with about 500 uF of smoothing capacitance 

Pulse generator and H-bridge inverter:

The 555 timer is visible towards the far left of the breadboard.
The rear MOSFETS drive the H-bridge transistors in the foreground

Below is a little demo of the H-bridge's operating principle:

Flyback transformers:

A small, non-standard HV flyback, rated at 9 kV. Feeds into the CW multiplying rectifier pictured later.

A more traditional HV flyback, salvaged from an old CRT. Output is rectified internally.

CW voltage multiplying rectifiers:

Uses low ESL "doorknob" capacitors. DC output is nominally four times the AC input.

First Setup: No Success Yet

I have finally constructed and tested my planned version of the charging and discharging circuits. Unfortunately, I haven't gotten the circuit working properly; the circuit is functional, but can't induce a water explosion.

Below is a picture of my implementation of the charging circuit.

  
The leftmost breadboard holds the switching and control circuit. The silver box to its right is a  high-voltage neon sign inverter; it takes in 12 VDC and puts out 2 kV @ 60 kHz. The inverter powers a rectifying voltage multiplier (on the second breadboard). The circuit essentially consists of several Greinacher voltage doublers (described in the previous post) stacked on top of each other. The circuit is commonly known as a Cockroft-Walton (CW) voltage multiplier. It is named after physicists John Cockroft and Ernest Walton, who discovered the circuit in 1932 and used it to power their atom smasher. At no load, the output voltage is theoretically twice the peak input voltage times the number of Greinacher stages in the circuit. A simple two stage CW multiplier is shown below. If, for example, the circuit was powered by a 3 kVp AC source, the open-circuit output would theoretically be 12 kV DC.

The actual output is significantly less than the theoretical output, and decreases with increasing load current. The 5-stage CW multiplier used in my charging circuit should theoretically produce 30 kV at no load; the actual output is a little more than 10 kV.

The CW multiplier is connected through two 25 MOhm resistors to two special reed relays at the far right of the picture. The relays are each rated at 5 kV and are used to connect the charging circuit to the capacitor bank. 

The whole apparatus is mounted on top of a sealable plastic container lined with tin foil. Inside the container are the capacitor bank and discharge switching mechanism.

The plastic bin serves to insulate the capacitor bank from the circuit's operator. The tin foil lining is meant to act as a Farady cage. The capacitor bank's discharge is often accompanied by some arcing near the switching mechanism's electrodes; the tin foil Farady cage is there to neutralize the electromagnetic field generated by the arcs. This prevents the radio noise from interfering with oscilloscope measurements.

The obscure "switching mechanism" I referenced in the previous paragraph has consisted of two different devices over the course of this project. The first is a system of relays similar to the big red ones used in the charging circuit. These relays are switched manually when the voltage across the capacitor bank reaches the desired level. The second switching device is a much cruder spark-gap switch that breaks down at a certain voltage, determined (partly) by the spark gap's length (as well as by electrode shape, air moisture, and a slew of other factors). The former switching mechanism was eventually replaced by the latter because the relays didn't handle the capacitors' high-current discharges very well (to say the least: they may or may not still work).

I've also experimented with a couple different types of capacitors. The picture below shows a high-voltage "slapper" capacitor, rated at 15 kV with a maximum underdampened discharge current of >2 kA (yikes!). The capacitor is discharged using the spark gap switch described above.

When the discharge switch is closed, the capacitor bank is discharged through the water accelerator barrel. The accelerator is shown below, in actual and diagrammatic representation:

The accelerator's actual dimension turned out to be a lot smaller than those given in the diagram. Instead of 12 cm x 9 cm, the accelerator is approximately 5 cm x 3 cm. It's built from a couple of sections of 1/2" PVC pipe, a length of 6 AWG wire, and a 1 mm-thick aluminum sheet. It can hold up to 2 mL of water. 

During a discharge event, the voltage across the capacitor bank is measured using a specialty high-voltage voltmeter probe. The thing (pictured below) looks like it belongs on a Star Trek set, but it gets the job done. It has a 1000:1 attenuation ratio and an input impedance of 1 GOhm.

The discharge current is measured using a special current transformer, called a Rogowski coil, and an oscilloscope. The Rogowski coil produces an output voltage proportional to the rate of change of current through the wire it's wrapped around. To glean information about the current through the wire,  you can slap an integrator circuit on the end of your coil, or employ some other method of numerical integration.

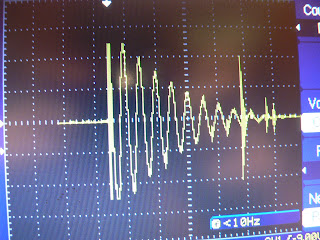
During a discharge event, the coil voltage usually looks something like this:

This waveform is from the discharge of my 6 kV 0.3 uF capacitor bank. The spike seen towards the end of the waveform is an illustration of the effects arc-generated radio noise have on oscilloscope measurements. From the waveform, the derivative of the discharge current dI/dt can be modeled as follows:

where Io is a placeholder value for the initial current (in this case it is actually a quantity in volts taken from the oscilloscope readout), tau is the discharge time constant (approximately one fifth the pulse width, in seconds), omega = 2*pi*f is the angular ringing frequency (with f, the ringing frequency, in hertz), and t is time, in seconds. Integrating yields:

It's assumed here that the constant of integration is zero. If you want to double check this answer, I'll let you do the integration by parts yourself. Note that the proportionality constant of the Rogowski coil is negative, so it will flip the signs of the current waveform around. The above equation describes a waveform shaped similarly to the one seen in the oscilloscope screenshot. This derived equation for I(t) will be used to describe the current waveforms of discharges during this experiment.

In the case of the waveform shown above, Io = 24.6 V, tau = 56 uS/5 = 11.2 uS, f = 192 kHz, and omega = 2*pi*192 kHz = 1206 kHz. I(t) is minimized on the interval [0, inf) when t = 0, so the maximum discharge current will be the current at I(0). From our model for the Rogowski coil output, I(0) is:

Note that this quantity is in volt-seconds. Since the proportionality constant of our Rogowski coil is -1.1758 x 10^(-8) ohm-seconds, the actual discharge current is:

that is, 1.7 kA. Apparently, this isn't quite enough current to get any water to explode. To rectify this, I'm planning on revamping my charging circuit to increase the capacitor charging voltage (more power!). This should help increase the peak discharge current.

The results of my second attempt at the water explosion apparatus will be posted here shortly.    

Discharge Circuit Design

My latest work on the project has centered around the assembly and testing of my charging and discharging circuits. Below is a diagram of the circuit I ultimately implemented for charging and discharging my capacitor bank (click for larger resolution).

When the DPST mechanical switch S1 is thrown to the left, the leftmost DPDT relay S2 is actuated. This then turns the step-up converter on and actuates the SPST charging relay S3. The capacitor C towards the bottom right of the diagram is then charged to the converter's output voltage (approx 6 kV) through the 1.2M resistor. Once the capacitor is fully charged (if C = 0.3 uF, RC = .36 s and the capacitor C will be charged to within 1% of its charging voltage in 5RC = 1.8 s), S1 is thrown to the right, actuating the SPST discharging relay S4 and shorting the capacitor's positive plate to ground. The resultant pulse discharge can be used to initiate a water arc explosion.


The diodes in parallel with each relay are there to protect the switch S1 (and the contacts of relay S2) from the momentary voltage spike produced when the relays are switched off. Relays S3 and S4 must be specially made for switching HV signals. I used two 5kV reed relays connected in series for both S3 and S4. The reed relays are designed so that their contacts are contained in an evacuated chamber, thus allowing them to switch high voltage without sparks arcing between the contacts.


The box labeled "DC-AC-DC Step-Up Converter" will likely comprise the below circuit.

The unit after the step-up inverter is called a Greinacher voltage doubler; it takes an AC signal and outputs DC (with ripple) at twice the peak input voltage. The first capacitor is charged on the negative half of the AC  cycle to the AC peak voltage. On the positive half, the output is a superposition of the input AC waveform onto the capacitor's discharge current. The second capacitor reduces voltage ripple.

The circuit's open-circuit output is nominally 2Vp. Under load, the circuit's output voltage drops with load impedance. The circuit's exact voltage characteristics are given by

Where I(load) is the current through the load (A), f is the frequency of the AC input (Hz), and C is the capacitance of the doubling capacitor (F). Assuming a maximum load current of 6kV/1.2MOhm = 5 mA, an input frequency of 60 kHz, and an input capacitance of 270 pF, the circuit's minimum output voltage comes out as 5691.4 V. As the capacitor C charges, I(load) will decay to zero, and the output voltage will level off at 6 kV.