Below is a picture of my implementation of the charging circuit.
The leftmost breadboard holds the switching and control circuit. The silver box to its right is a high-voltage neon sign inverter; it takes in 12 VDC and puts out 2 kV @ 60 kHz. The inverter powers a rectifying voltage multiplier (on the second breadboard). The circuit essentially consists of several Greinacher voltage doublers (described in the previous post) stacked on top of each other. The circuit is commonly known as a Cockroft-Walton (CW) voltage multiplier. It is named after physicists John Cockroft and Ernest Walton, who discovered the circuit in 1932 and used it to power their atom smasher. At no load, the output voltage is theoretically twice the peak input voltage times the number of Greinacher stages in the circuit. A simple two stage CW multiplier is shown below. If, for example, the circuit was powered by a 3 kVp AC source, the open-circuit output would theoretically be 12 kV DC.
The actual output is significantly less than the theoretical output, and decreases with increasing load current. The 5-stage CW multiplier used in my charging circuit should theoretically produce 30 kV at no load; the actual output is a little more than 10 kV.
The CW multiplier is connected through two 25 MOhm resistors to two special reed relays at the far right of the picture. The relays are each rated at 5 kV and are used to connect the charging circuit to the capacitor bank.
The plastic bin serves to insulate the capacitor bank from the circuit's operator. The tin foil lining is meant to act as a Farady cage. The capacitor bank's discharge is often accompanied by some arcing near the switching mechanism's electrodes; the tin foil Farady cage is there to neutralize the electromagnetic field generated by the arcs. This prevents the radio noise from interfering with oscilloscope measurements.
The obscure "switching mechanism" I referenced in the previous paragraph has consisted of two different devices over the course of this project. The first is a system of relays similar to the big red ones used in the charging circuit. These relays are switched manually when the voltage across the capacitor bank reaches the desired level. The second switching device is a much cruder spark-gap switch that breaks down at a certain voltage, determined (partly) by the spark gap's length (as well as by electrode shape, air moisture, and a slew of other factors). The former switching mechanism was eventually replaced by the latter because the relays didn't handle the capacitors' high-current discharges very well (to say the least: they may or may not still work).
I've also experimented with a couple different types of capacitors. The picture below shows a high-voltage "slapper" capacitor, rated at 15 kV with a maximum underdampened discharge current of >2 kA (yikes!). The capacitor is discharged using the spark gap switch described above.
When the discharge switch is closed, the capacitor bank is discharged through the water accelerator barrel. The accelerator is shown below, in actual and diagrammatic representation:

The accelerator's actual dimension turned out to be a lot smaller than those given in the diagram. Instead of 12 cm x 9 cm, the accelerator is approximately 5 cm x 3 cm. It's built from a couple of sections of 1/2" PVC pipe, a length of 6 AWG wire, and a 1 mm-thick aluminum sheet. It can hold up to 2 mL of water.
The discharge current is measured using a special current transformer, called a Rogowski coil, and an oscilloscope. The Rogowski coil produces an output voltage proportional to the rate of change of current through the wire it's wrapped around. To glean information about the current through the wire, you can slap an integrator circuit on the end of your coil, or employ some other method of numerical integration.
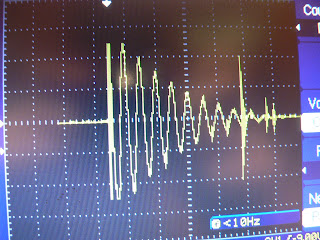
During a discharge event, the coil voltage usually looks something like this:
This waveform is from the discharge of my 6 kV 0.3 uF capacitor bank. The spike seen towards the end of the waveform is an illustration of the effects arc-generated radio noise have on oscilloscope measurements. From the waveform, the derivative of the discharge current dI/dt can be modeled as follows:
where Io is a placeholder value for the initial current (in this case it is actually a quantity in volts taken from the oscilloscope readout), tau is the discharge time constant (approximately one fifth the pulse width, in seconds), omega = 2*pi*f is the angular ringing frequency (with f, the ringing frequency, in hertz), and t is time, in seconds. Integrating yields:
It's assumed here that the constant of integration is zero. If you want to double check this answer, I'll let you do the integration by parts yourself. Note that the proportionality constant of the Rogowski coil is negative, so it will flip the signs of the current waveform around. The above equation describes a waveform shaped similarly to the one seen in the oscilloscope screenshot. This derived equation for I(t) will be used to describe the current waveforms of discharges during this experiment.
In the case of the waveform shown above, Io = 24.6 V, tau = 56 uS/5 = 11.2 uS, f = 192 kHz, and omega = 2*pi*192 kHz = 1206 kHz. I(t) is minimized on the interval [0, inf) when t = 0, so the maximum discharge current will be the current at I(0). From our model for the Rogowski coil output, I(0) is:
Note that this quantity is in volt-seconds. Since the proportionality constant of our Rogowski coil is -1.1758 x 10^(-8) ohm-seconds, the actual discharge current is:
that is, 1.7 kA. Apparently, this isn't quite enough current to get any water to explode. To rectify this, I'm planning on revamping my charging circuit to increase the capacitor charging voltage (more power!). This should help increase the peak discharge current.
The results of my second attempt at the water explosion apparatus will be posted here shortly.
The results of my second attempt at the water explosion apparatus will be posted here shortly.